Turbulence Modelling with Artificial Neural Networks

During my MEng in Mechanical at Imperial College London, I explored the potential of applying artificial neural networks (ANNs) for turbulence modelling under the supervision of Dr. Salvador Navarro-Martinez and alongside a classmate, Alvaro Prat Balasch.

Summary

Turbulence in fluid dynamics, described as “the most important unsolved problem of classical physics” by physicist Richard Feynman in 1964 -whose quote is still relevant today- is a particular case of a greater concept called deterministic chaos. Turbulence arises in a wide range of fluid flows: from flows around cars and aeroplanes to greater geophysical scales such as ocean currents or atmospheric flows.

The dynamics of these flows are described by the partial differential Navier-Stokes equations. These equations can be solved numerically for specific types of flows, but are computationally expensive and unviable for highly turbulent flows.

A method called Large Eddy Simulations (LES) spatially averages the Navier-Stokes equation to resolve only the large scales of motion of the flows, reducing the compurational power required.However, the averaging process gives rise to an additional stress component which incorporates small-scale terms of motion and must be modelled.

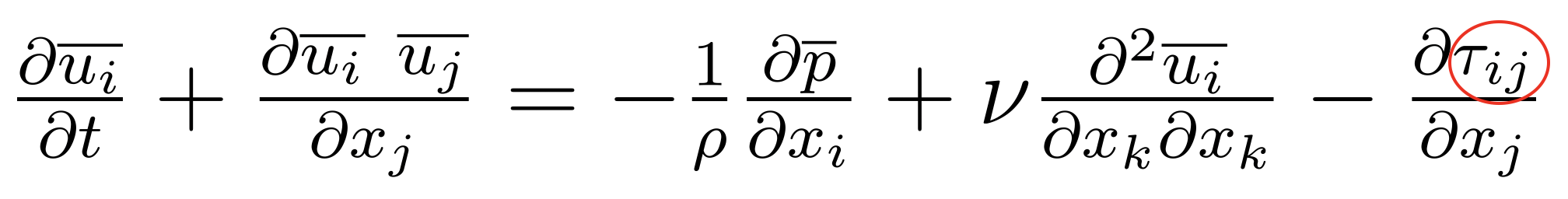
The spatially averaged Navier-Stokes. The terms correspond to the usual meanings in the field of Fluid Dynamics which will not be discussed here. The term circled in red is the residual stress term which must be modelled to predict the fluid's motion.

In our research, we model the residual stress term using ANNs and features from the large scales of motions, such as the flow velocity or the velocity gradient in space. The residual stress term being non-linear, hence the ability of ANNs to model non-linear functions suggested its potential in closing the filtered Navier-Stokes Equations.

Using similar features, we obtained correlation coefficeints superior to various classical turbulence models, for different types of turbulent flows: Homegenous Isotropic Turbulence, Buoyancy driven flows, Magnetohydrodyanmic flows, Channel Flows.

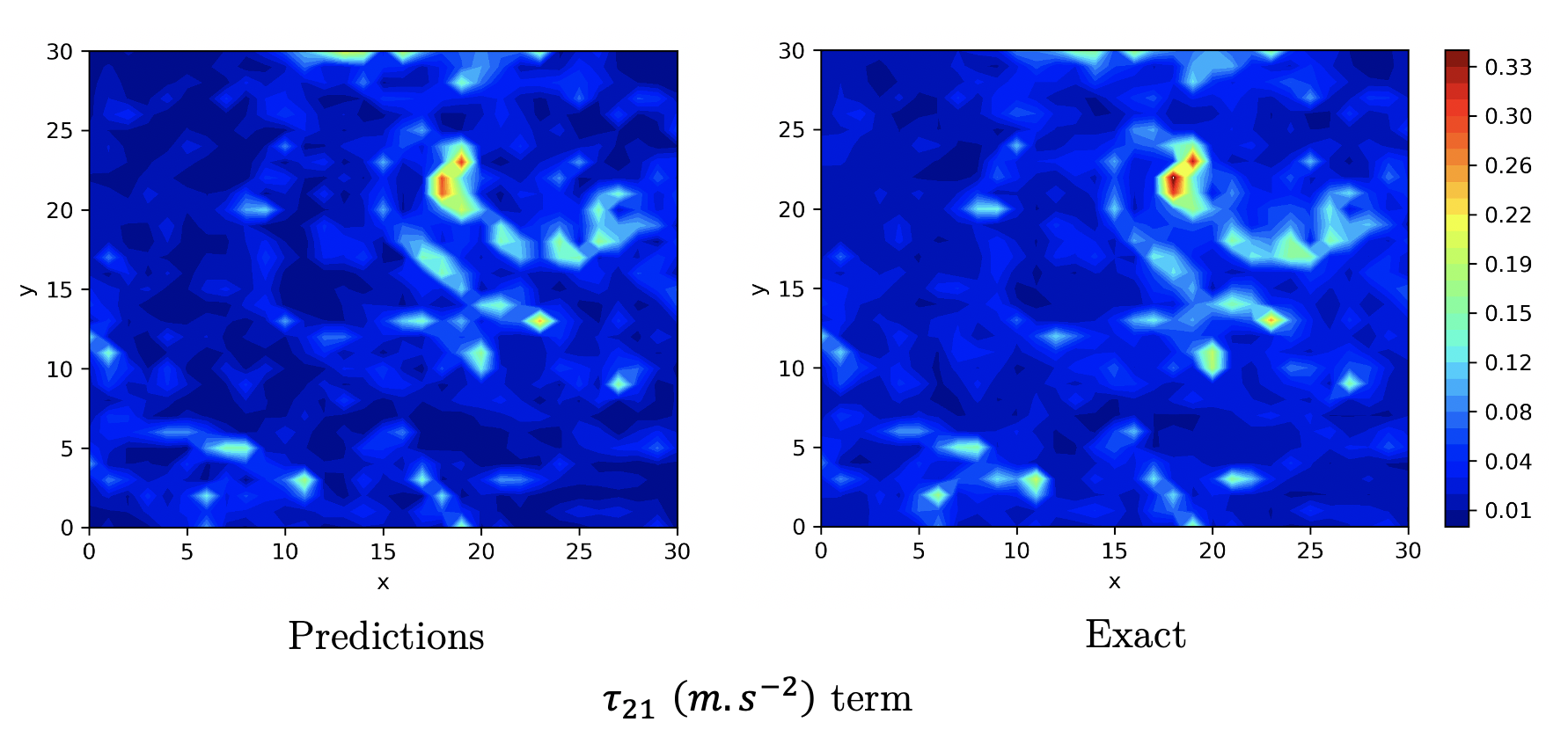
Example of the predictions of a residual stress term on a plane of a buoyancy mixing turbulent flow. A correlation coefficient of 0.92 between predicted and exact terms for such flows. The model manages to learn a model to predict the small scale residual stress term from large scales of motion features.

Find our publication in the International Journal of Computational Fluid Dynamics for a more in-depth technical description of the problem and our approach.